SPSS

Pengertian SPSS 

          SPSS adalah sebuah program aplikasi yang memiliki kemampuan analisis statistik cukup tinggi serta sistem manajemen data pada lingkungan grafis dengan menggunakan menu-menu deskriptif dan kotak-kotak dialog yang sederhana sehingga mudah untuk dipahami cara pengoperasiannya. Beberapa aktivitas dapat dilakukan dengan mudah dengan menggunakan pointing dan clicking mouse.

         SPSS banyak digunakan dalam berbagai riset pemasaran, pengendalian dan perbaikan mutu (quality improvement), serta riset-riset sains. SPSS pertama kali muncul dengan versi PC (bisa dipakai untuk komputer desktop) dengan nama SPSS/PC+ (versi DOS). Tetapi, dengan mulai populernya system operasi windows. SPSS mulai mengeluarkan versi windows (mulai dari versi 6.0 sampai versi terbaru sekarang). [1]

Langkah Analisis Mencari Statistika Deskriptif

Tabel 1 Data Nilai Mahasiswa (bukan data sebenarnya)

Nama	Usia	Jenis Kelamin	Nilai APK	Nilai PPC	Nilai PLO
Suhairi	20	Laki-Laki	80	50	70
Ambon	21	Laki-Laki	70	70	90
Astri	22	Perempuan	60	80	70
Henri	21	Laki-Laki	80	90	60
Yugos	22	Laki-Laki	90	60	70
Muji	19	Perempuan	70	80	80
Tatang	20	Laki-Laki	60	70	40
Ferdi	21	Laki-Laki	60	90	60
Arsyad	21	Laki-Laki	70	70	40
Fauzan	21	Laki-Laki	90	80	60

*) Laki-Laki (Value: 1), Perempuan (Value: 2)

Langkah pertama yang perlu dilakukan adalah meng-entry data, tentunya anda perlu paham dasar-dasar SPSS. Entry data dilakukan pada tab sheet Data View setiap baris mewakili  satu responden, sedangkan setiap kolom mewakili  satu variabel, dalam kasus ini variabelnya adalah: Nama, Usia, Jenis Kelamin, Nilai APK, Nilai PPC, dan Nilai PLO. Berikut langkah-langkah entry datanya:

• Masukkan variabel: Nama untuk “Nama”, Usia untuk “Usia”, Gender untuk “Jenis Kelamin”, APK untuk “Nilai APK”, PPC untuk “Nilai PPC”, dan PLO untuk “Nilai PLO” pada kolom Name pada tab sheet [Variable View].
• Berilah label untuk masing-masing variabel dengan menuliskannya pada kolom Label: Usia, Jenis Kelamin, Nilai APK, Nilai PPC, dan Nilai PLO. Hal ini berarti: variabel Gender mempunyai label “Jenis Kelamin”, variabel APK mempunyai label “Nilai APK”, dan seterusnya.
• Untuk variabel Gender pada kolom Values, definisikan Value: 1 = Laki-laki dan Value: 2 = Perempuan.
• Untuk variabel Nama (baris pertama ) pada kolom Type, ubah tipe data menjadi String.
• Pada kolom Decimals isi nol untuk semua variabel.
• Untuk kolom lainnya seperti Width, Missing, dan Columns biarkan tetap default SPSS.
• Jangan lupa ”save”  atau tekan Ctrl + S. Secara default SPSS akan memberi nama file: data_1.sav, saya merubah nama file menjadi eRiskProject_1.sav.

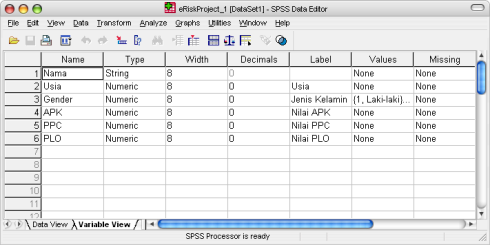
Gambar 1. Entry Variabel pada Tab Sheet Variable View

• Kemudian klik tab sheet [Data View] dan mulailah meng-entry data seperti yang diperlihatkan Gambar 2 di bawah ini.

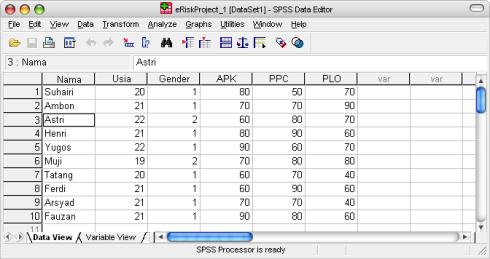
Gambar 2. Entry Data pada Tab Sheet Data View

• Untuk melihat hasil definisi Value pada variabel Gender, klik ikon , variabel Gender akan terdefinisi menjadi laki-laki dan perempuan, tidak lagi berisi angka 1 dan 2.
• Selanjutnya, kita ingin menjumlahkan nilai APK, PPC, dan PLO, Klik menu [Transform] –> [Compute], muncul dialog box Compute Variable.
• Buatlah variabel baru dengan nama “total” untuk menempatkan hasil penjumlahan nilai APK, PPC, dan PLO, caranya: tuliskan “total” pada form Target Variable. Kemudian Klik [Type & Label], beri label “Nilai Total“.
• Ketik “APK + PPC + PLO” (sesuai nama variabel dan perintah penjumlahan ) pada form Numeric Expression. Anda juga dapat menggunakan tombol-tombol yang tersedia pada dialog box, lihat Gambar 3.

Gambar 3. Contoh Perintah Penjumlahan pada Dialog Box Compute Variable

• Klik [OK]. Pada Data View akan muncul variabel baru dengan nama “Total” (lihat Gambar 4).

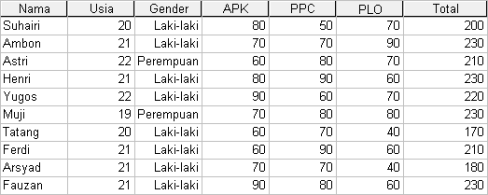
Gambar 4. Output dari Perintah Penjumlahan pada Dialog Box Compute Variable 

Setelah data di-entry, selanjutnya memulai menggunakan perintah-perintah statistik deskriptif

Dengan menggunakan data sebelumnya langkah-langkah perintah Descriptives adalah sebagai berikut:

• Klik menu [Analyze] -> [Descriptives Statistics] -> [Descriptives].
• Muncul dialog box Descriptives. Masukkan variabel yang akan dianalisis ke form Variables(s). Untuk melakukan setting optional klik [Options].
• Muncul dialog box Descriptives: Options. Centang analisis yang diperlukan. Dalam hal ini pilihannya adalah: Mean, Std. deviation, Minimum, Maximum, Kurtosis, Skewness, dan pada form Display Order centang Variable list.

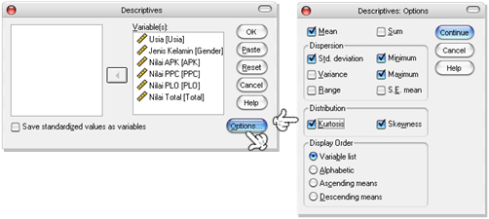
Gambar 9. Langkah-Langkah Descriptives Statistics

• Klik [Continue] dan [OK]. Hasil analisis akan terlihat seperti tabel yang ditunjukkan Gambar 10 di bawah ini:

Gambar 10. Output Descriptives

Tabel output di atas menunjukkan jumlah pengukuran (N), nilai minimum (Minimum), nilai maksimum (Maximum), nilai rata-rata (Mean), standar deviasi (Std.), Skewness, dan Kurtosis dari masing-masing variabel. Nilai skewness merupakan ukuran kesimetrisan histogram, sedangkan kurtosis merupakan ukuran datar atau runcingnya histogram. Idealnya nilai skewness dan kurtosis pada distribusi normal adalah nol. Oleh karena itu:

• Jika nilai skewness positif maka distribusi data “miring ke kiri distribusi normal” (ada frekuensi nilai yang tinggi di sebelah kiri titik tengah distribusi normal), sebaliknya apabila skewness negatif maka distribusi data ”miring ke kanan distribusi normal” (kiri bagi kita yang melihatnya).
• Jika nilai kurtosis positif maka distribusi data “meruncing” (ada satu nilai yang mendominasi), sebaliknya apabila Kurtosis Negatif maka distribusi data “melandai” (varians besar).

Perhatikan Gambar 10 di atas, variabel Usia memiliki skewness negatif dan kurtosis positif, artinya distribusinya “miring ke kiri distribusi normal” dan “meruncing”. Pada variabel nilai APK, nilai skewness positif dan nilai kurtosis negatif, artinya distribusinya “miring ke kanan distribusi normal” dan “melandai”. Sebagai pembuktian, buat histogram untuk variabel Usia dan Nilai APK. Berikut caranya:

• Klik menu [Graphs] -> [Histogram], maka muncul dialog box Histogram.
• Pilih variabel Usia dan masukkan dalam form Variable.
• Centang Display normal curve, untuk memperlihatkan kurva normal.
• Selanjutnya klik [OK]. [2]

Langkah Analisis Mencari Korelasi 

Perlu diingat :

Koefisien Korelasi akan selalu berada di dalam Range -1 ≤ r ≤ +1

Jika ditemukan perhitungan diluar Range tersebut, berarti  telah terjadi kesalahan perhitungan dan harus di koreksi terhadap perhitungan tersebut.

Rumus Pearson Product Moment

Koefisien Korelasi Sederhana disebut juga dengan Koefisien Korelasi Pearson karena rumus perhitungan Koefisien korelasi sederhana ini dikemukakan oleh Karl Pearson yaitu seorang ahli Matematika yang berasal dari Inggris.

Rumus yang dipergunakan untuk menghitung Koefisien Korelasi Sederhana adalah sebagai berikut :
(Rumus ini disebut juga dengan Pearson Product Moment)

r =               nΣxy – (Σx) (Σy)                   
.         √{nΣx² – (Σx)²} {nΣy² – (Σy)²}

Dimana :

n    = Banyaknya Pasangan data X dan Y
Σx = Total Jumlah dari Variabel X
Σy = Total Jumlah dari Variabel Y
Σx²= Kuadrat dari Total Jumlah Variabel X
Σy²= Kuadrat dari Total Jumlah Variabel Y
Σxy= Hasil Perkalian dari Total Jumlah Variabel X dan Variabel Y

Pola / Bentuk Hubungan antara 2 Variabel  :

1. Korelasi Linear Positif  (+1)

Perubahan salah satu Nilai Variabel diikuti perubahan Nilai Variabel yang lainnya secara teratur dengan arah yang sama. Jika Nilai Variabel X mengalami kenaikan, maka Variabel Y akan ikut naik. Jika Nilai Variabel X mengalami penurunan, maka Variabel Y akan ikut turun.

Apabila Nilai Koefisien Korelasi mendekati +1 (positif Satu) berarti pasangan data Variabel X dan Variabel Y memiliki Korelasi Linear Positif yang kuat/Erat.

2. Korelasi Linear Negatif (-1)

Perubahan salah satu Nilai Variabel diikuti perubahan Nilai Variabel yang lainnya secara teratur dengan arah yang berlawanan. Jika Nilai Variabel X mengalami kenaikan, maka Variabel Y akan turun. Jika Nilai Variabel X mengalami penurunan, maka Nilai Variabel Y akan naik.

Apabila Nilai Koefisien Korelasi mendekati -1 (Negatif Satu) maka hal ini menunjukan pasangan data Variabel X dan Variabel Y memiliki Korelasi Linear Negatif yang kuat/erat.

3. Tidak Berkorelasi (0)

Kenaikan Nilai Variabel yang satunya kadang-kadang  diikut dengan penurunan Variabel lainnya atau kadang-kadang diikuti dengan kenaikan Variable yang lainnya. Arah hubungannya tidak teratur, kadang-kadang searah, kadang-kadang berlawanan.

Apabila Nilai Koefisien Korelasi mendekati 0 (Nol) berarti pasangan data Variabel X dan Variabel Y memiliki korelasi yang sangat lemah atau berkemungkinan tidak berkorelasi.

Ketiga Pola atau bentuk hubungan tersebut jika di gambarkan ke dalam Scatter Diagram (Diagram tebar) adalah sebagai berikut :

Tabel tentang Pedoman umum dalam menentukan Kriteria Korelasi :

r	Kriteria Hubungan
0	Tidak ada Korelasi
0 – 0.5	Korelasi Lemah
0.5 – 0.8	Korelasi sedang
0.8 – 1	Korelasi Kuat / erat
1	Korelasi Sempurna

Contoh Penggunaan Analisis Korelasi di Produksi :

1. Apakah ada hubungan antara suhu ruangan dengan jumlah cacat Produksi?
2. Apakah ada hubungan antara lamanya waktu kerusakan mesin dengan jumlah cacat produksi?
3. Apakah ada hubungan antara jumlah Jam lembur dengan tingkat absensi?

Contoh Kasus Analisis Korelasi Sederhana :

Seorang Engineer ingin mempelajari apakah adanya pengaruh Suhu Ruangan terhadap Jumlah Cacat yang dihasilkan dan juga ingin mengetahui keeratan serta bentuk hubungan antara dua variabel tersebut. Engineer tersebut kemudian mengambil data selama 30 hari terhadap rata-rata (mean) suhu ruangan dan Jumlah Cacat Produksi seperti dibawah ini :

Tanggal	Rata-rata Suhu Ruangan	Jumlah Cacat
1	24	10
2	22	5
3	21	6
4	20	3
5	22	6
6	19	4
7	20	5
8	23	9
9	24	11
10	25	13
11	21	7
12	20	4
13	20	6
14	19	3
15	25	12
16	27	13
17	28	16
18	25	12
19	26	14
20	24	12
21	27	16
22	23	9
23	24	13
24	23	11
25	22	7
26	21	5
27	26	12
28	25	11
29	26	13
30	27	14

Penyelesaian :

Pertama-tama hitunglah X², Y², XY dan totalnya seperti tabel dibawah ini :

Tanggal	Rata-rata Suhu Ruangan (X)	Jumlah Cacat    (Y)	X2	Y2	XY
1	24	10	576	100	240
2	22	5	484	25	110
3	21	6	441	36	126
4	20	3	400	9	60
5	22	6	484	36	132
6	19	4	361	16	76
7	20	5	400	25	100
8	23	9	529	81	207
9	24	11	576	121	264
10	25	13	625	169	325
11	21	7	441	49	147
12	20	4	400	16	80
13	20	6	400	36	120
14	19	3	361	9	57
15	25	12	625	144	300
16	27	13	729	169	351
17	28	16	784	256	448
18	25	12	625	144	300
19	26	14	676	196	364
20	24	12	576	144	288
21	27	16	729	256	432
22	23	9	529	81	207
23	24	13	576	169	312
24	23	11	529	121	253
25	22	7	484	49	154
26	21	5	441	25	105
27	26	12	676	144	312
28	25	11	625	121	275
29	26	13	676	169	338
30	27	14	729	196	378
Total	699	282	16487	3112	6861

Kemudian hitunglah Koefisien Korelasi berdasarkan rumus korelasi dibawah ini :

r =               nΣxy – (Σx) (Σy)                    
.          √{nΣx² – (Σx)²} {nΣy² – (Σy)²}

r =                   (30 . 6861) – (699) (282)                     
.          √{30. 16487 – (699)²} {30 . 3112 – (282)²}

r =                    (205830) – (197118)                          
.          √{494610 – 488601} {93360 – 75924}

r =               8712          
.                9118.13

r =   0.955

Jadi Koefisien Korelasi antara Suhu Ruangan dan Jumlah Cacat Produksi adalah 0.955, berarti kedua variabel tersebut memiliki hubungan yang ERAT dan bentuk hubungannya adalah Linear Positif.

Jika Hubungan Suhu Ruangan dan Jumlah Cacat Produksi dibuat dalam bentuk Scatter Diagram (Diagram Tebar), maka bentuknya akan seperti dibawah ini :

Analisis Korelasi (Correlation Analysis) juga merupakan salah satu alat (tool) yang digunakan dalam Metodologi Six Sigma di Tahap Analisis.

Untuk mempermudah kita dalam Menghitung Koefisien Korelasi, kita juga dapat menggunakan Microsoft Excel. Silakan kunjungi : “Cara Menghitung Koefisien Korelasi dengan menggunakan Microsoft Excel” untuk mengetahui langkah-langkah perhitungannya. [3]

Langkah Analisis Mencari Regresi

         

1. Input data ke SPSS.

Ada 2 view dalam SPSS, yaitu Data View dan Variable View. Data di input ke Data View. 

Sementara Variable View digunakan untuk memberi nama variabel. 

2. Tahap selanjutnya yaitu analisis regresi. Untuk melakukan analisis Regresi Sederhana, pilih menu Analyze, lalu Regression dan klik Linear. 

Setelah muncul kotak dialog, pindahkan variabel Nilai Impor ke kotak Dependent dan variabel Pendapatan Nasional ke kotak Independent(s). Klik OK.

Ini hasil analisis Regresi Sederhana

3. Untuk melakukan analisis Regresi Ganda. Pilih menu Analyze, lalu Regression dan klik Linear. Setelah muncul kotak dialog, pindahkan variabel Tahun ke kotak Dependent, sedangkan variabel Nilai Impor dan Pendapatan Nasional ke kotak Independent(s). Klik Statistics. Aktifkan box Collinearity diagnostics dan klik Continue. Klik OK.

Ini hasil analisis Regresi Ganda

NB : Setiap selesai melakukan analisis, hasil analisisnya di save. Setelah semuanya selesai, data yang diinput pertama kali juga di save. [4]

REFERENSI :

[1] https://soehusaeni.wordpress.com/2010/06/08/apa-itu-spss/

[2] https://eriskusnadi.wordpress.com/2008/12/11/statistik-deskriptif-dengan-spss/
[3] http://teknikelektronika.com/pengertian-analisis-korelasi-sederhana-rumus-pearson/
[4] http://dianindahlestari41.blogspot.co.id/